Rope Technology
Rope
Characteristics
Breaking strength
The calculated breaking strength of a steel wire rope is defined as the metallic cross section of a steel wire rope (the sum of the individual cross sections of all the wires making up the rope) multiplied by the nominal tensile strength of the steel wire rope. The minimum breaking strength of the steel wire rope is the calculated breaking strength of the rope multiplied by the spin factor.
The actual breaking strength of a steel wire rope is the breaking strength of the rope as determined in a pull test. A new steel wire rope must achieve an actual breaking strength equal to or higher than the minimum breaking strength. The breaking strength of a steel wire rope can be increased by increasing the metallic area of the rope (e.g. by using strands with higher fill factors, by compacting the strands or by swaging the rope), by increasing the tensile strengths of the individual wires or by increasing the spin factor of the rope. This can also be achieved by improving the contact conditions between the rope elements by using a plastic infill.
Bending fatigue resistance
The bending fatigue resistance of steel wire ropes is defined as the number of bending cycles a rope can achieve in a bending fatigue test under defined parameters (e.g. running over sheaves with a defined diameter and a predetermined line pull corresponding to the MBL of the steel wire rope). The bending fatigue resistance of the steel wire rope increases with increasing D/d ratio (= sheave diameter (D): nominal rope diameter (d)) and by reducing the line pull. The bending fatigue resistance of a steel wire rope can be increased by increasing the contact area between the steel wire rope and the sheave and by increasing the contact conditions between the rope elements, by adding a plastic layer between the IWRC and the outer strands. Due to the larger contact area between the ropes and the sheaves and due to the increased flexibility, 8- strand ropes are more resistant to bending fatigue than 6- strand ropes of a similar design.
Flexibility
The flexibility of a steel wire rope typically increases with increasing a number of strands and wires in the rope. The flexibility is also influenced by the lay lengths of the strands, of the rope core and the rope as well as by the gaps between wires and strands. If a rope is not flexible enough, it will have to be forced to bend around a sheave of a given diameter, which will reduce the bending fatigue life of the rope. It will also be forced to bend around a drum of a given diameter. Spooling problems might be a consequence.
Efficiency Factor
When running over a sheave a rope has to be converted from a straight condition into a bent condition at the point when the rope runs onto the sheave and has to be converted again from the bent into the straight condition when it runs off the sheave. Also the bearing has to be turned. In doing so, the friction forces in the rope as well as the friction forces in the bearing have to be overcome. This leads to a change of the rope force. One describes the relationship of the rope force on both sides of the sheave as the efficiency factor and accepts that this numerical value also takes into account the friction losses of the bearing. When measuring the efficiency factor of a rope the loss of the line pull while the rope is running over the sheave is measured. An efficiency factor of 0,98, or alternatively a strength loss of 2%, is generally assumed for wire ropes.
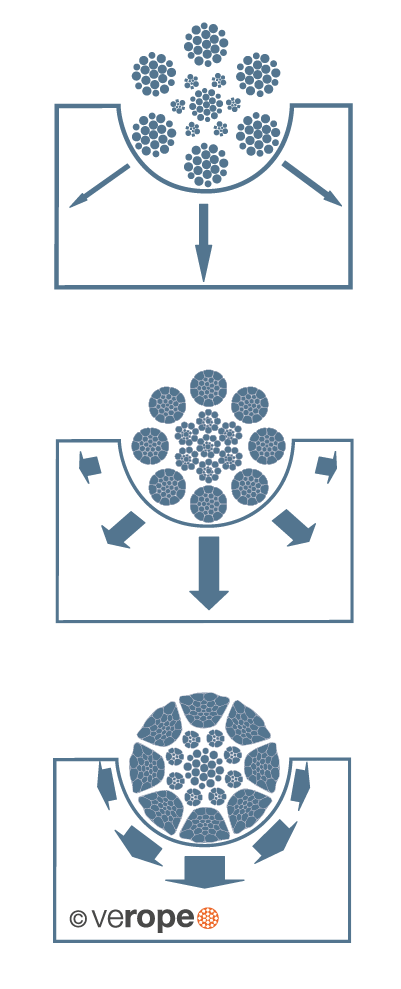
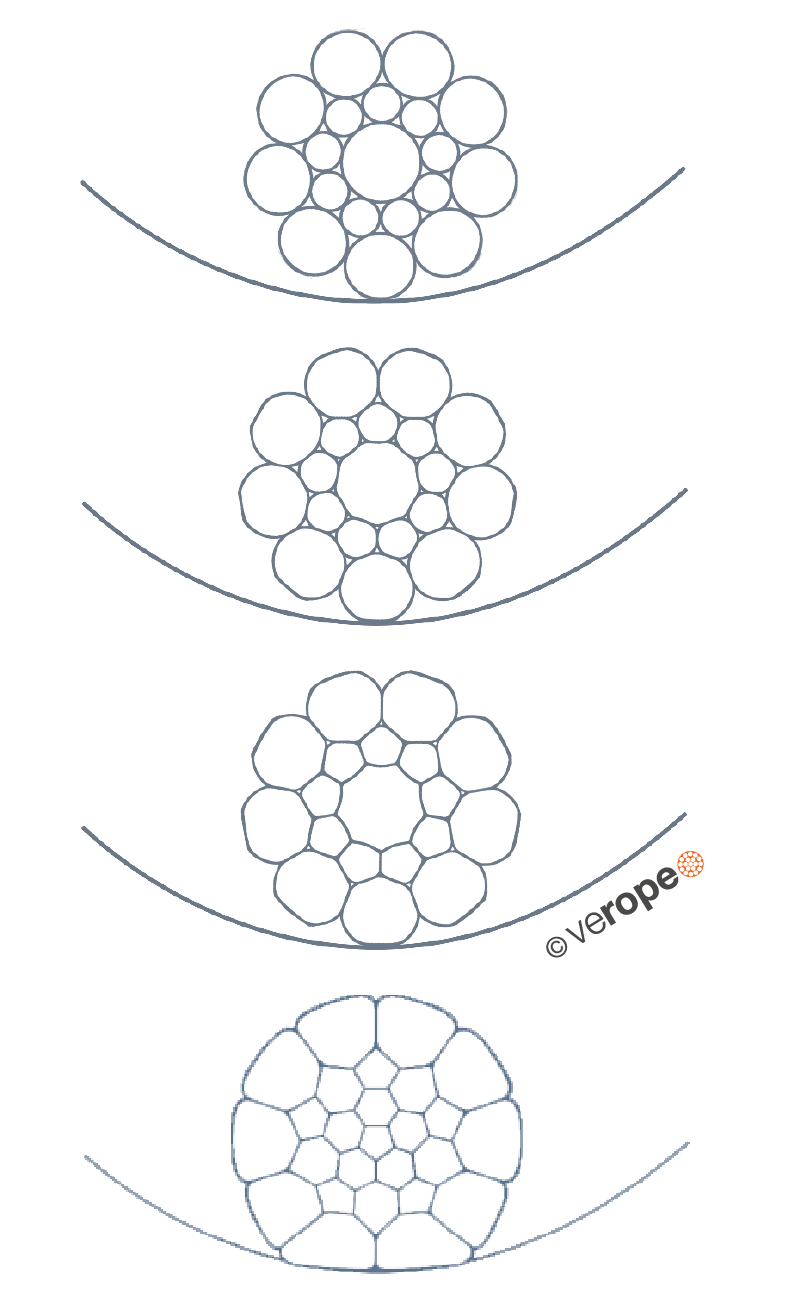
ISO rope with conventional outer strands
veropro 8 with compacted outer strands
veropower 8 with compacted and rotary swaged outer strands
Wear resistance
Changes in line pull will cause changes in the rope length. Rope sections lying on a sheave or on the first wraps of a drum can only adapt to the changing line pull by sliding over the groove surface of the sheave or the drum when the length change occurs. This relative motion will cause abrasion (both in the grooves and on the special wire rope). Using less and therefore larger outer wires can increase the wear resistance of the rope.
The pressure between the sheave and the rope can be minimized due to optimized contact areas; therefore also the wear of the rope can be minimized (figure 24). The wear resistance can also be influenced by the metallurgy of the outer strands.
Unique special wire ropes
Uniquely by:
- high quality wire rod
- state of the art design
- experienced production & innovative rope tests
- careful development due computerized wire rope sizing
- manufactured by the world’s largest wire product manufacturers using the latest machinery
- due to Kiswire’s own wire drawing the raw material is of unsurpassed quality
- unique design
Deformation Behavior
➜ Modulus of elasticity The modulus of elasticity of a material is defined as the proportional factor between load and elongation.
The modulus of elasticity is a material property. Besides the elastic properties of the wire material used, the modulus of elasticity of wire ropes is dependent on the rope geometry and the load history of the rope. Since this is not a material property, ISO 12076 recommends calling this factor the “rope modulus”.
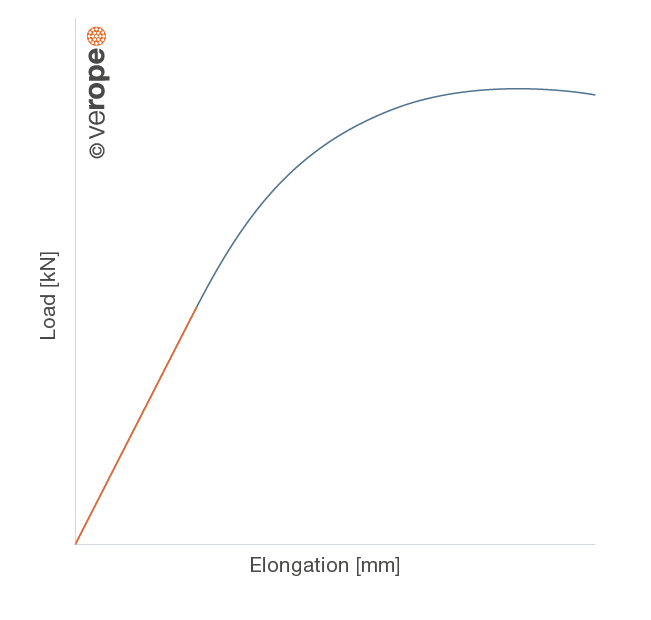
Figure 25 shows a load-elongation diagram of a wire. Here the modulus of elasticity can be determined as the gradient of the curve in the linear area.
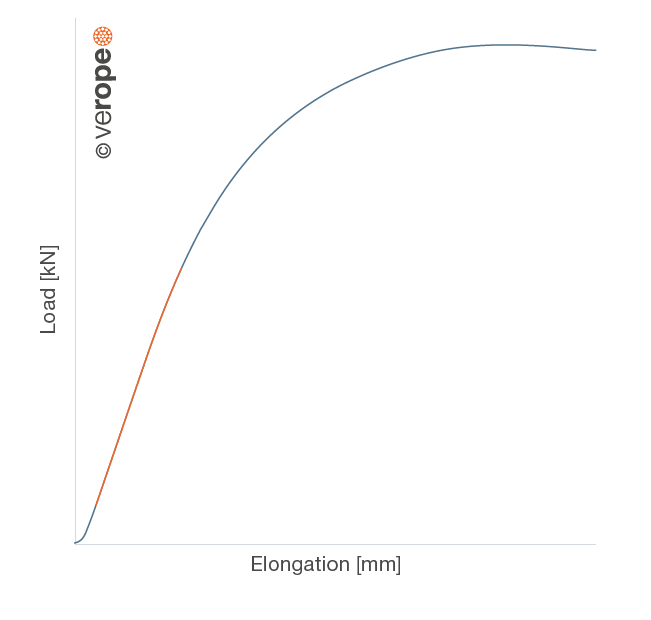
Figure 26 shows a load-elongation diagram of a strand. As the strand consists of several wires of different lengths and different lay lengths or different lay angels, here the shorter and less elastic elements get loaded first. For this reason the curve is not linear in the lower area. The strand only gets linear, when all the wires in the strand bear the load together.
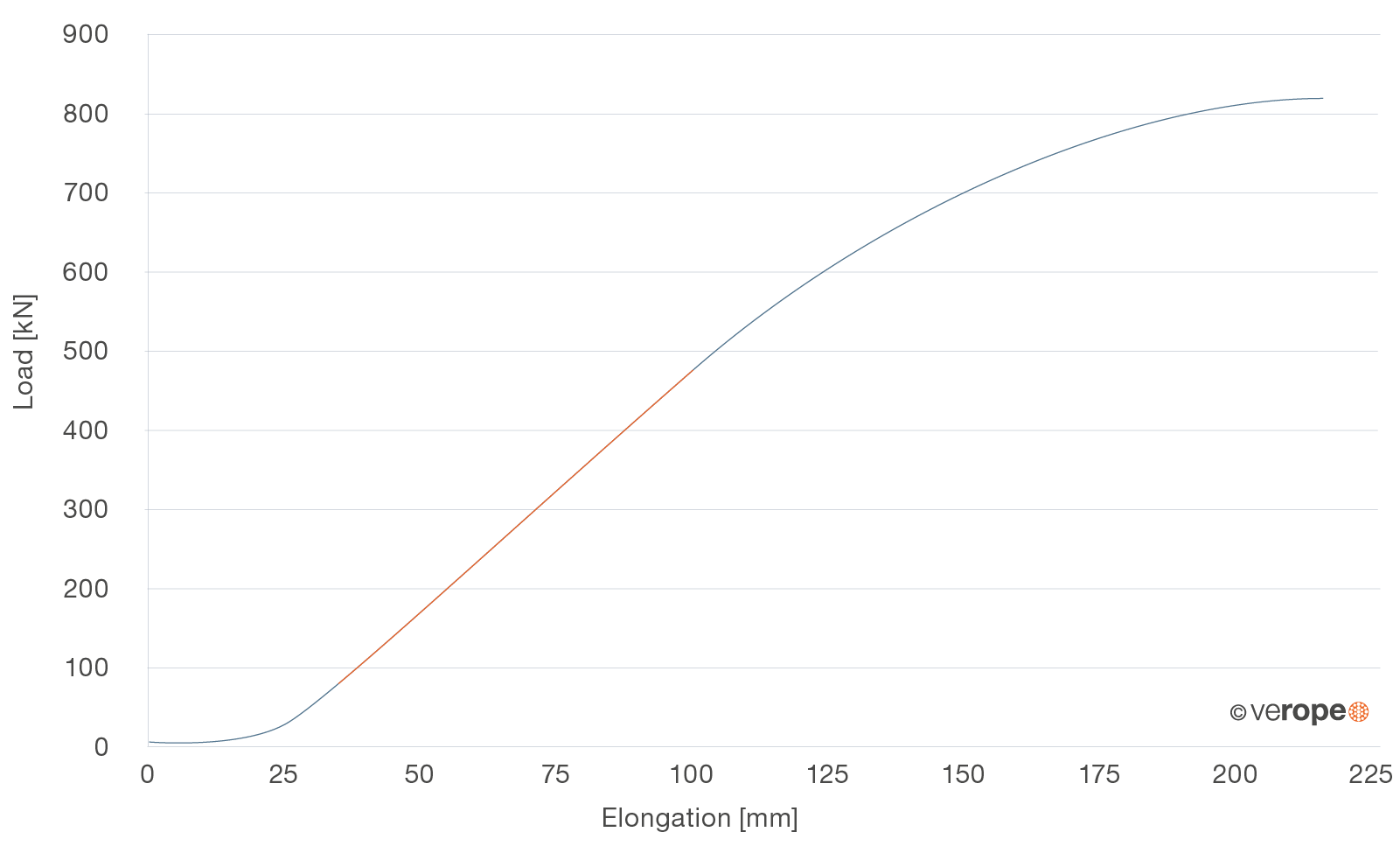
Figure 27 shows the load-elongation diagram of a rope. Here you will also find a non-linear correlation in the lower area between load and elongation. Here again the nonlinearity explains itself by the overload of the shorter and the less elastic rope elements. The load-elongation diagram is linear in the area in which all elements share the load and do not yet flow. As a consequence of settling effects, the modulus of elasticity of wire ropes increases over the lifetime. The biggest part of this change happens with the first loading of the rope. Later the modulus of elasticity varies only very slightly. For this reason a new wire rope should always be loaded and relived multiple times before measuring the modulus of elasticity. The determination of the modulus of elasticity is described in ISO 12076.